개요
특정 값[A]을 기준으로 (A 앞은 A 값 이하의 값들)[B]을, (A 뒤는 A 값 이상의 값들)[C]을 배치한다.
이를 각각 B와 C에 대해 재귀적으로 실행하면 결국 전체에 대해 정렬하게 된다.
복잡도
| 최악 | 평균 | 최소 | |
|---|---|---|---|
| Big O 표기법 | O(n^2) | O(n log n) | O(n log n) |
알고리즘 절차
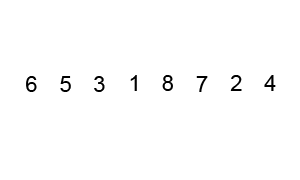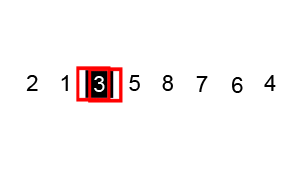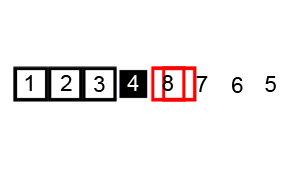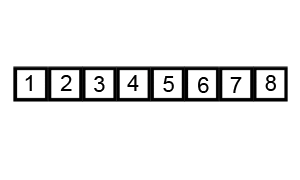
- 임의의 특정 값[A]을 기준으로 잡고 A를 제외한 부분의 양쪽 값부터 검사를 진행한다.
즉, 포인터 start와 end를 설정해 특정 규칙에 맞게 start와 end 인덱스의 값들을 Swap한다.
특정 규칙이란, A값을 기준으로 특정 인덱스[pivot]을 기준으로 pivot 앞의 요소들은 A값보다 작아야 하고 pivot 뒤의 요소들은 A값보다 커야 한다는 것을 의미한다. - 포인터 start는 맨 앞의 요소부터 시작해서 A값보다 작다면 정상적인 값이기 때문에 그냥 +1을 해서 지나간다.
하지만 start 위치의 값이 A값보다 크다면 바꾸기 위해 잠시 진행을 멈춘다. - 포인터 end는 맨 뒤의 요소부터 시작해서 A값보다 크다면 정상적인 값이기 때문에 그냥 -1을 해서 지나간다.
하지만 end 위치의 값이 A값보다 작다면 바꾸기 위해 잠시 진행을 멈춘다. - 두 포인터의 진행이 모두 멈춘다면 두 위치를 Swap한다. 그리고 다시 2번부터 진행한다.
- 만약 두 포인터의 위치가 역전된다면 모든 자리가 특정 위치를 기준으로 A값보다 크고 작은 것이기 때문에 루프를 진행하지 않는다. 그리고 이 때의 end 포인터의 값 이후는 A값보다 무조건 큰 값이므로 이 값을 return해서 다음 과정에서 사용할 수 있도록 함.
- pivot값을 기준으로 그 이전의 부분 집합[B]과 그 이후의 부분 집합[C]에 대해 또 1번 부터 5까지의 과정을 다시 겪음.
- 이 과정을 B, C의 크기가 1이 될 때까지 반복함.
자바 코드
class Quick {
public static void main(String[] args) {
int[] testCase1 = {1, 26, 9, 67,653,452,2,3,46,87,356543};
quickSort(testCase1, 0, testCase1.length-1);
for (int item : testCase1) {
System.out.println(item);
}
}
public static void quickSort(int[] arr, int low, int high) {
if(high<=low) return ;
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot-1);
quickSort(arr, pivot+1, high);
}
public static int partition(int[] arr, int low, int high) {
int pivot = high;
int start = low;
int end = high - 1;
while(start < end) {
if(arr[start] <= arr[pivot]) {
start++;
} else if (arr[pivot] < arr[end]) {
end--;
} else {
swap(arr, start, end);
}
}
if(arr[end] > arr[pivot]) {
swap(arr, end, pivot);
pivot = end;
} return pivot;
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}