다익스트라

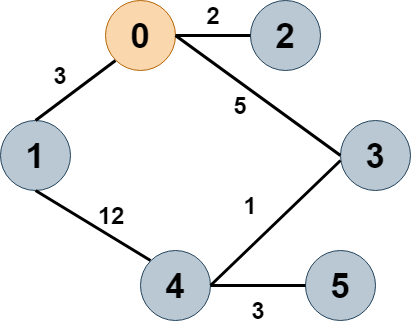
👣 개요

특정 노드에서 나머지 모든 노드로의 최단거리를 계산하는 알고리즘

최단 경로 문제를 해결하기 위한 그래프 탐색 알고리즘.
그리디 알고리즘가 쓰여 매 순간 가장 최단거리만 선택해서 계산한다.

이 알고리즘을 사용하려면 음의 가중치를 가지지 않은 그래프여야 한다.
여기서 음의 가중치라는 것은 경로를 움직일 때마다
Cost가 늘어나야지 줄어들면 안 된다는 것이다.

---

👣 복잡도

	평균
Big O 표기법	O((V + E)logV)

V는 노드 갯수, E는 그래프 간선 수

---

👣 알고리즘 절차

1. 그래프의 시작 노드를 선택합니다.
2. 시작 노드에서부터의 시작 노드의 거리는 0으로 설정합니다. 나머지 노드들의 거리는 무한대(infinity)로 초기화합니다.
3. 시작 노드를 포함한 모든 노드들을 탐색하기 위해 다음 과정을 반복합니다:
   • 아직 방문하지 않은 노드들 중에서 가장 거리가 짧은 노드를 선택합니다. 초기에는 시작 노드를 선택합니다.
   • 선택한 노드의 인접한 노드들을 탐색하면서, 시작 노드를 통해 해당 노드로 가는 거리를 계산합니다. 기존에 저장된 거리보다 짧은 거리를 발견하면, 해당 거리로 업데이트합니다.
4. 모든 노드들을 방문할 때까지 3번의 과정을 반복합니다.

---

👣 코드 예시

from heapq import heappop, heappush

def dijkstra(graph, start):
    # 시작 노드까지의 거리는 0
    # 나머지 노드까지의 거리는 Inf
    distances = {node: float('inf') for node in graph}
    distances[start] = 0
    
    heap = [(0, start)]
    
    while heap:
        current_distance, current_node = heappop(heap)
        
        # 이미 처리된 노드인 경우 건너뛰기
        if current_distance > distances[current_node]:
            continue
        
        for neighbor, weight in graph[current_node].items():
            distance = current_distance + weight
            
            # 거리가 업데이트되지 않으면 스킵.
            if distance >= distances[neighbor]:
                continue
            distances[neighbor] = distance
            
            # 우선순위 큐에 추가
            heappush(heap, (distance, neighbor))
    
    return distances

graph = {
    'A': {'B': 5, 'C': 2},
    'B': {'D': 1, 'E': 6},
    'C': {'F': 8},
    'D': {},
    'E': {'F': 3},
    'F': {},
}

start_node = 'A'
distances = dijkstra(graph, start_node)

# output - 결과의 형태만 표기한 것이지 거리값은 틀릴 수 있음.
# distances = {
    'A': 0,
    'B': 2,
    'C': 3,
    'D': 1,
    'E': 3,
    'F': 5,
}