👣 개요
기존의 복잡한 문제를 간단한 작은 문제로 나눠 점차 해결해나가는 문제 풀이법.
점화식을 세우고 초기값을 이용해 원하는 목표를 달성한다.
👣 적용 사례 1 - 프로그래머스 '도둑질'
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
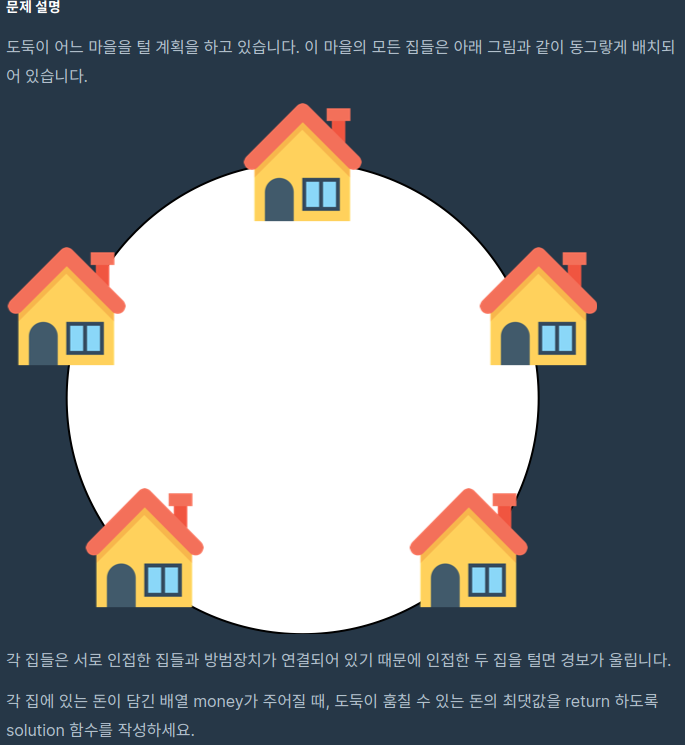

이 문제는 점화식을 다음과 같이 설정했다.
F(n) = max( F(n-1) , F(n-2) + money[n] )
F(n) : n 번째까지의 갈취한 돈의 최대값.
(n 까지 턴 돈) = (n-1 까지 턴 돈)과 (n-2까지 털고 n을 턴 돈) 중 더 많은 돈.
그리고 초기값은 2가지 상황을 상정해 설정했다.
시나리오 1)
첫 번째를 털고 / 2번째를 털지 못하고 / 마지막(n)을 털지 못하는 상황.
F(0) = F(1) = money[0], F(n-1) = F(n)
시나리오 2)
첫 번째를 털지 않고 / 2번째를 터는 상황.
F(0) = 0, F(1) = money[0]
def solution(money):
F = [None] * len(money)
G = [None] * len(money)
# 첫 번째 집을 털고 시작. (시나리오 1 - F)
F[0], F[1] = money[0], money[0]
# 첫 번째 집을 털지 않고 시작. (시나리오 2 - G)
G[0], G[1] = 0, money[1]
for n, item in enumerate(money[2:], start=2):
F[n] = max(F[n-1], F[n-2] + item)
G[n] = max(G[n-1], G[n-2] + item)
# (시나리오 1)과 (시나리오 2) 중 더 많이 턴 돈 찾기.
# 시나리오 1 : 이미 첫번째 집을 털었기에 F[-1]는 털 수 없다.
# 시나리오 2 : 첫번째 집을 안 털었기에 G[-1]는 털어도 된다.
return max(F[-2], G[-1])👣 적용 사례 2 - 프로그래머스 '3 X n 타일링'
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

n이 홀수인 경우는 무조건 0 이므로 논의에서 제외.
n이 짝수인 경우는 여러가지로 경우의 수[F(n)]를 만들 수 있다.
1. F(n-2) 경우의 수에 F(2) 경우의 수 조합

2. F(n-4) 경우의 수에 2가지 경우의 수 조합.

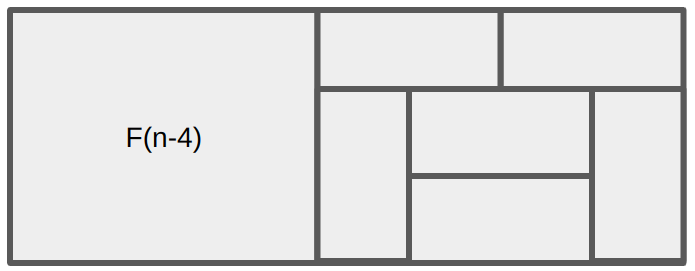
3. F(n-6) 경우의 수에 2가지 경우의 수 조합.
4. F(n-8) 경우의 수에 2가지 경우의 수 조합.
...
x. F(2) 경우의 수에 2가지 경우의 수 조합.
따라서 점화식을 다음과 같이 세울 수 있다.
F[i] = F[i-2] X F[2] + F[i-4] X 2 + F[i-6] X 2 + ... + F[2] X 2
F[i-2] = F[i-4] X F[2] + F[i-6] X 2 + ... + F[2] X 2
F[i] - F[i-2] = F[i-2] X F[2] + (2 - F[2]) X F[i-4]
따라서,
F[i] = (F[2] + 1) X F[i-2] + (F[2] - 2) X F[i-4] = 4 x F[i-2] - 1 x F[i-4]
F[i] = 4F[i-2] - F[i-4] , F[2] = 3, F[4] = 11
def solution(n):
# 홀수는 무조건 0 출력
if n%2==1: return 0
# F[2], F[4] = 3, 11
tail, head = 3, 11
for _ in range(6, n+1, 2):
tail, head = head, (head * 4 - tail * 1)
return head % 1000000007